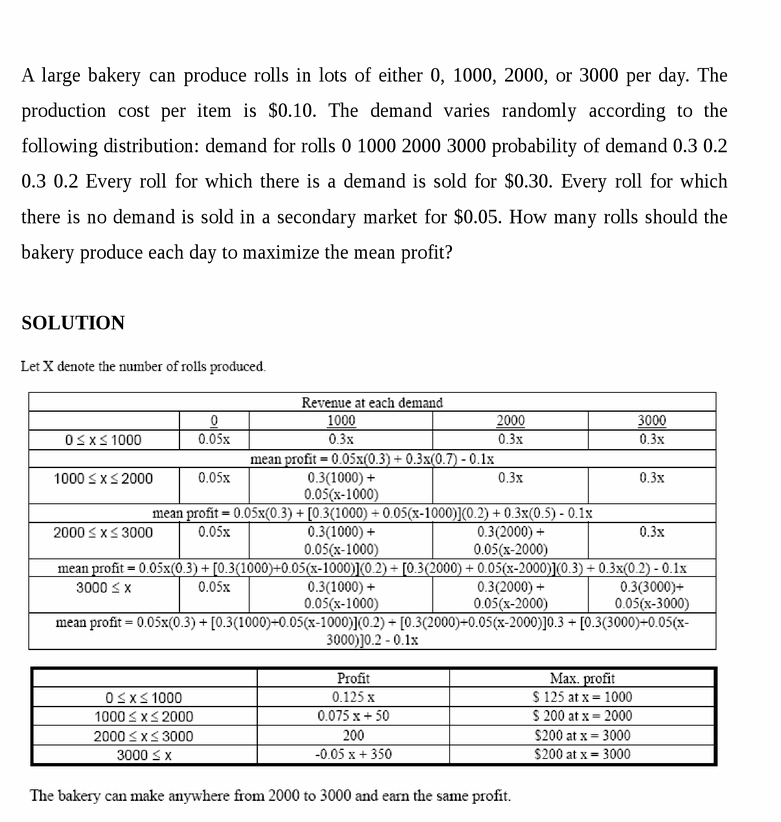
A large bakery can produce rolls in lots of either 0, 1000, 2000, or 3000 per day. The production cost per item is $0.10. The demand varies randomly according to the following distribution: demand for rolls 0 1000 2000 3000 probability of demand 0.3 0.2 0.3 0.2 Every roll for which there is a demand is sold for $0.30. Every roll for which there is no demand is sold in a secondary market for $0.05. How many rolls should the bakery produce each day to maximize the mean profit? |
| New search. (Also 1294 free access solutions) |